Waving Hands Dev Part 1: Spell Data Structure
This is the first development blog entry for the Waving Hands project I outlined in the last post.
As a starting point I wanted to look into how best to represent the options for spells. The goal is to create a data structure which allows me to update it (by pushing a new gesture) and on each update gives me back a new spell (if one was completed) or nothing.
For this post I’ll use the spells starting with the F (Wiggled Fingers) gesture in the examples:
| Gestures | Spell |
| F-F-F | Paralysis |
| F-P-S-F-W | Summon Troll |
| F-S-S-D-D | Fireball |
There are around 40 spells in total with 6 gestures composing them.
Trie Structure
My first idea was to use a Trie structure. This would mean creating a tree where at each node we either complete a spell or have a follow-up node for the selected gesture. If no follow-up exists we go back to the root node and start over.
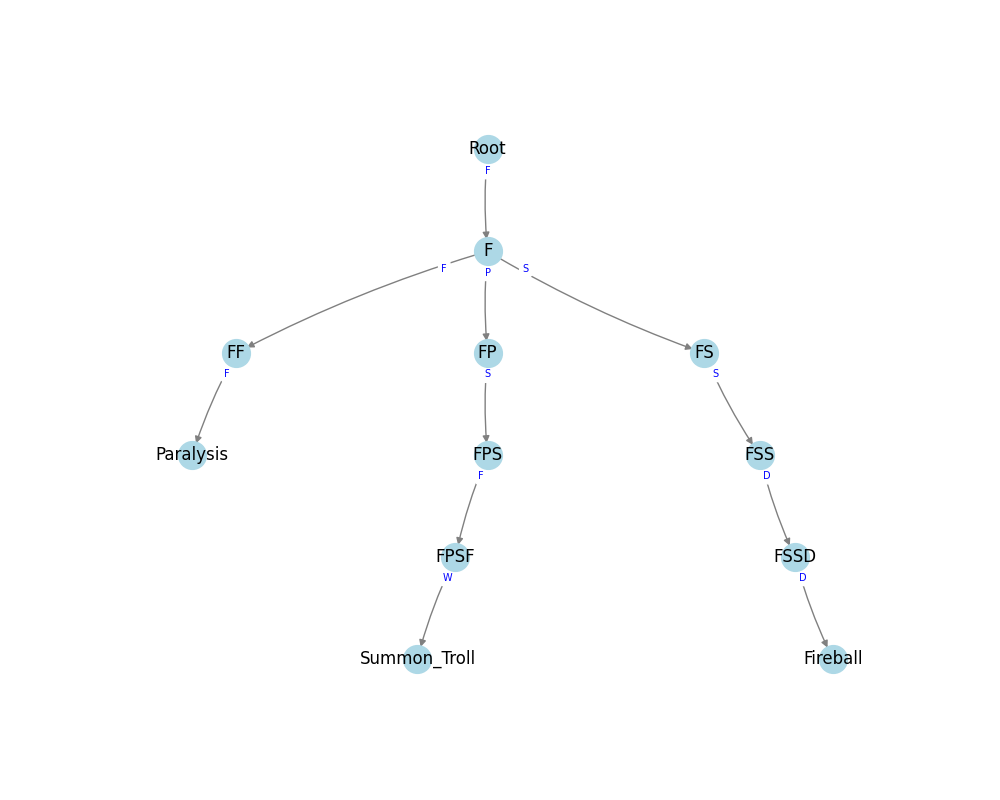
This approach is great for one-time casting, but does not cover cases where spells overlap. When we complete an F-F-F Paralysis spell the caster can immediately use the F gesture to complete another Paralysis spell without needing to go back to the start.
Paralysis is an extreme example of this overlap, but it is a common pattern, and adds strategic depth to the caster’s spell choices.
One way to work around this issue would be to maintain a window of trie’s. In the Paralysis example, we could have the F-F-F trie indicating the complete spell, but also trie’s in the F and F-F states which we can keep updating to detect subsequent spells.
I think this would work but it seems clunky and I’d prefer to have an all-in-one solution.
Spell State Machine
A cleaner approach is to create a state machine which covers all possible gesture transitions for a single hand.
In this state machine, two states are considered unique if they have different levels of progress towards at least one spell. The (Odin lang) code for each state currently looks like this:
Spell_State_Node :: struct {
// This is just handy for serialisation
id: int,
// The gesture that caused us to enter this state
previous_gesture: Maybe(Gesture_Type),
// Completed spell if there is one
spell: Maybe(Spell),
// States we can reach from here
next: [len(Gesture_Type)]Maybe(^Spell_State_Node),
// The progress (i.e. number of correct gestures) towards each spell
spell_progress: []int
}
We can perform a depth-first search to generate the state machine given the available spells. I won’t post the full code here (I’ll link it at the end) but in pseudo-code the recursive procedure looks like this:
PROCEDURE spell_state_machine_init(ssm: Spell_State_Machine,
spells: LIST of Spell)
root_node = new Spell_State_Node(id: 0, spell_progress: new LIST of 0s with length len(spells))
ssm.states = new SET with custom comparison based on spell_progress
ssm.root = ssm.states.add(root_node)
spell_state_machine_init_recursive(ssm, ssm.root, new LIST(), spells)
END PROCEDURE
PROCEDURE spell_state_machine_init_recursive(ssm: Spell_State_Machine,
current_node: Spell_State_Node,
gesture_stack: LIST of Gesture_Type,
spells: LIST of Spell)
FOR EACH gesture IN all_gestures DO
gesture_stack.append(gesture)
next_progress = copy_list(current_node.spell_progress)
next_spell = NONE
FOR spell_idx FROM 0 TO len(spells) - 1 DO
// Check how much of the spell prefix matches
current_spell = spells[spell_idx]
num_matches = 0
FOR n FROM 1 TO len(current_spell.gestures) DO
IF len(gesture_stack) >= n AND
gesture_stack[last n elements] == current_spell.gestures[first n elements] THEN
num_matches = n
END IF
END FOR
next_progress[spell_idx] = num_matches
IF num_matches == len(current_spell.gestures) THEN
next_spell = current_spell
END IF
END FOR
potential_next_node = new Spell_State_Node(spell: next_spell, spell_progress: next_progress)
actual_next_node, inserted_new = ssm.states.add_or_get(potential_next_node)
current_node.next[gesture] = actual_next_node
IF inserted_new THEN
// Explore the new state.
spell_state_machine_init_recursive(ssm, actual_next_node, gesture_stack, spells)
END IF
gesture_stack.pop_back()
END FOR
END PROCEDURE
Odin
I’ve chosen to go with Odin lang for this first development stage.
I find Odin to be a fun language to program in. It’s got a rich standard library, making it faster to develop applications than C, but still has manual memory managment (with a few extra conveniences, like a selection of pre-made allocators and the defer keyword) so gives absolute control over performance.
A convenient feature for this particular task was the ability to write unit tests on the fly in the same file as the code being tested.
Odin has great interoperability with C via its FFI (foreign function interface) so expect the final codebase to be a mixture of languages.
The resulting state machine which supports all of the spells is very complex, containing 112 distinct states. I haven’t found a good way to render this in a readable way, but can do a pretty good job with our reduced spell set containing just the F-* spells:
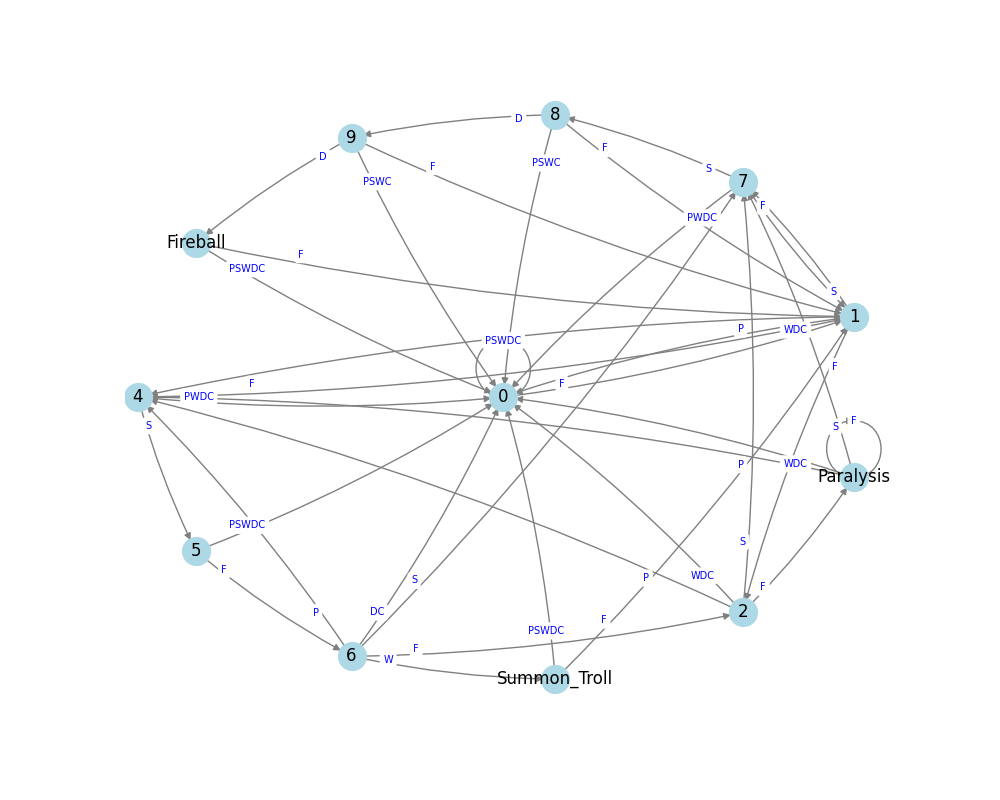
In this diagram:
- The
0state in the centre is the starting point. In this state there’s no progress towards any spells in the set.- The only way to leave this state is via the
Fgesture because all spells start with it.
- The only way to leave this state is via the
- For each edge the label is near the originating state. So for example, we have two edges between states 1 & 7, and the
Sgesture triggers the transition going from 1 to 7,Fis going in the other direction. - We can see what once we’re in the Paralysis state the
Fgesture does not cause a state transition - we remain in this state.
Drawing the graphs
The trie & state machine graphs were produced with a Python script that takes in an edges file (see the serialise function for the Spell_State_Machine) and uses the networkx module with matplotlib to render it.
The key steps were to:
- Pick the right graph type (
MultiDiGraph) - Play around with the layout type and the edge connection style to get the best result
State Machine Limitations
There are a few aspects of the spell casting process that aren’t captured by the current state machine approach.
- We’re only modelling one hand. In theory I guess it’s possible to have a single state machine which keeps track of both hands, but I think this would be prohibitively large. It should be easy to keep track of the hands independently and then do some extra checks if a spell requires both hands to perform.
- I excluded the Surrender “spell” (performed by double-
P). This isn’t really a spell, and because the incantation is so short it would add a lot of extra state transitions. I think this is better handled elsewhere. - “Double-spell” scenarios. I didn’t realise this before, but it’s actually quite common to complete two spells on the same turn, even with a single hand! The
Pgesture is all that’s needed to cast a Shield, and there are multiple other spells that end withP. I need to check the rules, but I think in these scenarios it makes sense for the player to be able to choose which spell they cast. This would mean the states need to be extended to support multiple spell options.
Conclusions & Code
I’m happy with state machine solution: the remaining limitations all seem very tractable.
This commit was authored at the time this article was written, so the code references should be one-to-one. Specifically you’ll want to take a look at the spell_state_machine.odin file. Chances are things will look significantly different in later commits.